Review of Complex Numbers

Cartesian Form and the Complex Plane

• Complex numbers and functions contain the number $i = \sqrt{-1}$.

• Any complex number or function $z$ can be written in Cartesian form,

  \[\label{eq:z} z = a + i b\]

  where $a$ is the real part of $z$ and $b$ is the imaginary part of $z$, often denoted $a = Re{z}$ and $b = Im{z}$, respectively. Note that $a$ and $b$ are both real numbers.

• The form of Eq. 1 is called Cartesian, because if we think of $z$ as a two dimensional vector and $Re{z}$ and $Im{z}$ as its components, we can represent $z$ as a point on the complex plane.

  

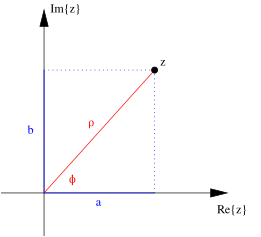
Polar Form

• As with a two dimensional vector, a complex number can be written in a second form, as a magnitude $\rho$ and angle $\phi$,

  \[\rho = \sqrt{a^2 + b^2}\] \[\tan \phi = \frac{b}{a} ~~(+ \pi~\mathrm{if}~a<0)\] \[a = \rho \cos \phi\] \[b = \rho \sin \phi.\]

  where $\phi$ is called the complex phase of $z$.

Exponential Form

• Euler’s formula relates a complex number on the unit circle expressed in terms of trigonometric functions to the complex exponential function.

  \[\label{eq:Euler} e^{\pm i\phi} = \cos \phi \pm i \sin \phi.\]

  This can be shown by comparing the Taylor series expansions of $e^{i\phi}$, $\cos \phi$, and $\sin \phi$. It follows that a complex number $z$ can be written in a third form,

  \[\label{eq:zExp} z = \rho e^{i\phi}.\]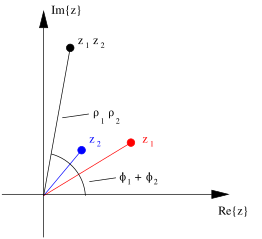

  

• Eq. 7 provides a useful way of looking at multiplication of complex numbers. The product $z_1 z_2$ is obtained by multiplying magnitudes and adding complex phases,

  \[z_1 z_2 = \rho_1 \rho_2 e^{i(\phi_1 + \phi_2)}.\]

• Raising complex numbers to powers is also simplified by Eq. 7

  \[\label{eq:zPow} (z)^p = \rho^p e^{i p \phi}.\]

  For example, we can evaluate $(i+1)^4$, noting that

  \[1+i = \sqrt{2} \, e^{i\frac{\pi}{4}}\]

  and using Eq. 9, we find

  \[(1+i)^4 = (\sqrt{2})^4 \, (e^{i\frac{\pi}{4}})^4 = 4 \, e^{i\pi} = -4\]

Complex Conjugation and the Complex Square

• The complex conjugate of $z = a + ib = \rho e^{i\phi}$ is

  \[z^* = a - ib = \rho e^{-i \phi}.\]

  It is obtained by changing the sign of $i$ wherever it appears in $z$.

  • To calculate the magnitude $\rho$ directly from $z$ written in any form, we use the complex square,

    \[|z|^2 = z^* z\]

    The complex square in terms of $a$ and $b$ is

    \[|z|^2 = (a + ib)(a - ib) = a^2 + iba - iab - (i^2)b^2 = a^2 + b^2 = \rho^2\]

    and in terms of $\rho$ and $\phi$

    \[|z|^2 = \rho e^{-i \phi} \rho e^{i \phi} = \rho^2.\]

    Hence,

    \[\rho = \sqrt{|z|^2}.\]

  • We can also use complex conjugation to separate the real and imaginary parts of $z$.

    \[z + z^* = a + ib + a - ib = 2a\]

    so

    \[\label{eq:Re} Re\{z\} = \frac{z + z^*}{2}\]

    similarly

    \[\label{eq:Im} Im\{z\} = \frac{z - z^*}{2i}\]

    For example, it follows from Eq.’s 18 and 19 together with Eq. 6 that

    \[\nonumber Re\{e^{i\phi}\} = \cos \phi = \frac{e^{i\phi} + e^{-i\phi}}{2}\] \[Im\{e^{i\phi}\} = \sin \phi = \frac{e^{i\phi} - e^{-i\phi}}{2i}\]

Finding Roots

• $\sqrt[n]{z}$ has $n$ unique values for integer $n$. For example, $\sqrt{4} = +2, -2$. In general, some or all of the $n$ roots are complex numbers.

• The cyclical nature of angles means that

  \[z = \rho e^{i\phi},\,\rho e^{i(\phi + 2\pi)}, \,\rho e^{i(\phi + 4\pi)}, \,\rho e^{i(\phi + 6\pi)}, ...\]

  all represent the same number.

• However, if we take the nth root of these representations of $z$, we find that there are $n$ unique results with complex phase angles less than $2 \pi$.

• Example

  • The first 6 representations of $z=8$ are

    \[8 = 8, \,8e^{i2\pi}, \,8e^{i4\pi}, \,8e^{i6\pi}, \, 8e^{i8\pi}, \,8e^{i10\pi}.\]

    Taking the 6th root, we obtain

    \[\sqrt[6]{8} = \sqrt{2}, \,\sqrt{2} e^{i \pi/3}, \,\sqrt{2} e^{i 2\pi/3}, \,\sqrt{2} e^{i \pi}, \,\sqrt{2} e^{i 4\pi/3}, \,\sqrt{2} e^{i 5\pi/3}\]

    The rest of the roots have complex phase $\geq 2\pi$ and all of them are alternate representations of the six roots above.

  • Graphically,

    

• In general, to find the $n$ roots of a number $z = \rho e^{i\phi}$, start with $\sqrt[n]{\rho} e^{i\phi/n}$. The remaining roots lie, along with the first, on a circle of radius $\sqrt[n]{\rho}$ in the complex plane at an equal spacing of $2\pi/n$ in phase angle.

This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License: http://creativecommons.org/licenses/by-sa/4.0/.
L.A. Riley (lriley@ursinus.edu), updated June 2021