Calculating Determinants

• The determinant of a $2 \times 2$ matrix

  \[M = \left( \begin{array}{cccc} m_{11} & m_{12} \\ m_{21} & m_{22} \end{array} \right)\]

  is given by

  \[|M| = \left| \begin{array}{cccc} m_{11} & m_{12} \\ m_{21} & m_{22} \end{array} \right| = m_{11} \, m_{22} - m_{12} \, m_{21}\]

• The determinant of a $3 \times 3$ matrix

  \[M = \left( \begin{array}{cccc} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array} \right)\]

  can be written in terms of the determinants of $2 \times 2$ sub-matrices

  \[|M| = \left| \begin{array}{cccc} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array} \right| \\ = m_{11} \left| \begin{array}{cccc} m_{22} & m_{23} \\ m_{32} & m_{33} \end{array} \right| \,-\, m_{12} \left| \begin{array}{cccc} m_{21} & m_{23} \\ m_{31} & m_{33} \end{array} \right| \,+\, m_{13} \left| \begin{array}{cccc} m_{21} & m_{22} \\ m_{31} & m_{32} \end{array} \right|\]

• In general, each element of the top row of the matrix is multiplied by the determinant of the sub-matrix obtained by removing the row and column containing that element. The results are then added together with alternating sign, starting with a positive $m_{11}$ term. Figure 1 shows the top-row elements and the associated sub-matrices and signs for the $2 \times 2$, $3 \times 3$, and $4 \times 4$ cases.

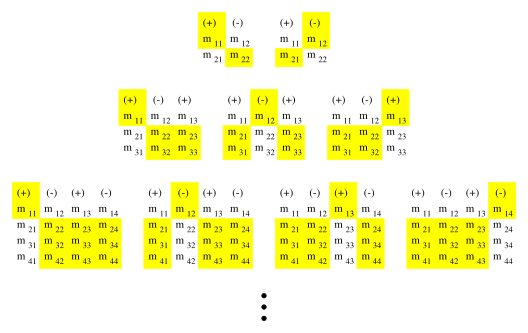
Figure 1: A visual guide to computing the determinants of $2 \times 2$, $3 \times 3$, and $4 \times 4$ matrices.

An $\mathbf{n=2}$ Example

\[M = \left( \begin{array}{cccc} 3 & -1 \\ 5 & 7 \end{array} \right)\] \[|M| = 3 \cdot 7 - (-1)\cdot 5 = 21 + 5 = 26\]

An $\mathbf{n=3}$ Example

\[M = \left( \begin{array}{cccc} 4 & 2 & 5 \\ -1 & 6 & 7 \\ 3 & 1 & 2 \end{array} \right)\] \[|M| = 4 \left| \begin{array}{cccc} 6 & 7 \\ 1 & 2 \end{array} \right| \,-\, 2 \left| \begin{array}{cccc} -1 & 7 \\ 3 & 2 \end{array} \right| \,+\, 5 \left| \begin{array}{cccc} -1 & 6 \\ 3 & 1 \end{array} \right|\] \[= 4 \, (6 \cdot 2 - 7 \cdot 1) - 2 \, ((-1) \cdot 2 - 7 \cdot 3) + 5 \, ((-1) \cdot 1 - 6 \cdot 3)\\ = 20 + 46 - 95 \\ = -29\]

This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License: http://creativecommons.org/licenses/by-sa/4.0/.
L.A. Riley (lriley@ursinus.edu), updated June 2021