The Quadratic Formula

• Equations of the form

  \[\label{eq:quadratic} ax^2 + bx + c = 0\]

  are called quadratic equations. The quadratic formula

  \[\label{eq:qFormula} x = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a}\]

  gives the solutions.

• The $\pm$ in Eq. 2 is an important detail. In general, there are two solutions to a quadratic equation. The two solutions are also called the roots of the equation.

• Example

  A ball is tossed directly upward from a height of 2.0 m above the ground with an initial velocity of 5.0 m/s. It is subject only to the force of gravity while in flight, so it has an acceleration of -9.8 m/s$^2$. When does the ball reach a height of 3.0 m? The position of the ball as a function of time is given by the equation

  \[y = y_o + v_o t + \frac{1}{2}a t^2.\]

  Solution

  The equation with the given information is

  \[3.0~\mathrm{m} = 2.0~\mathrm{m} + (5.0~\mathrm{m/s}) t + (-4.9~\mathrm{m/s}^2) t^2\]

  which in the form of Eq. 1 becomes

  \[\label{eq:example} (-4.9~\mathrm{m/s}^2) t^2 + (5.0~\mathrm{m/s}) t + (-1.0~\mathrm{m}) = 0.\]

  We can identify $a =-4.9~\mathrm{m/s}^2$, $b = 5.0~\mathrm{m/s}$, and $c = -1.0~\mathrm{m}$ and apply Eq. 2,

  \[t = -\frac{5.0~\mathrm{m/s}}{2(-4.9~\mathrm{m/s}^2)} \pm \frac{\sqrt{(5.0~\mathrm{m/s})^2 - 4(-4.9~\mathrm{m/s}^2)(-1.0~\mathrm{m})}} {2(-4.9~\mathrm{m/s}^2)} = 0.51~s \mp 0.24~s = 0.27~s, 0.75~s.\]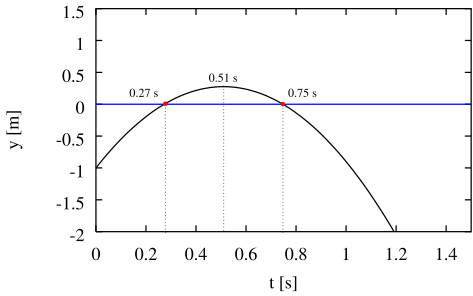

  

  Figure 1: The left side of Eq. 5 plotted vs. $t$.

  • To understand the two solutions, the graph of the left side of Eq. 5 shown in Fig. 1 is helpful. The extreme value of the quadratic occurs at $-\frac{b}{2a}$. In the example, the extreme value is at 0.51 s.

  • The roots of the quadratic lie $\frac{\sqrt{b^2 - 4ac}}{2a}$ to either side of $-\frac{b}{2a}$. In the example, the two roots of the equation lie 0.24 s to either side of 0.51 s.

  • A graph like this is often helpful in choosing appropriate solutions. In the example, both roots of the equation are appropriate. The ball reaches a height of 3.0 m twice, once going up, and once coming down.

• Special Cases

  • Single solution

    If $4ac = b^2$, then $\sqrt{b^2-4ac} = 0$, and there is only one solution, $x=-\frac{b}{2a}$. In the above example, this corresponds to 0.51 s, the time at which the ball reaches its maximum height.

  • Complex solutions

    If $4ac > b^2$, then $\sqrt{b^2-4ac}$ is imaginary (involves $i = \sqrt{-1}$). The above example does not have a physically reasonable solution corresponding to this situation. (This situation corresponds to heights never reached by the ball.)

This work is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License: http://creativecommons.org/licenses/by-sa/4.0/.
L.A. Riley (lriley@ursinus.edu), updated June 2021